Skip to main content

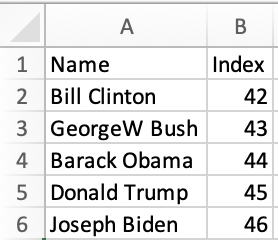
统计摘要

摘要统计数据可以帮助人们快速理解数据集并做出明智的决策。许多有趣的数据集都存储在电子表格文件中。

¥Summary statistics help people quickly understand datasets and make informed decisions. Many interesting datasets are stored in spreadsheet files.

SheetJS 是一个用于从电子表格读取和写入数据的 JavaScript 库。

¥SheetJS is a JavaScript library for reading and writing data from spreadsheets.

该演示使用 SheetJS 处理电子表格中的数据。我们将探讨如何提取电子表格数据以及如何计算简单的汇总统计数据。该演示将重点关注两种通用数据表示形式：

¥This demo uses SheetJS to process data in spreadsheets. We'll explore how to extract spreadsheet data and how to compute simple summary statistics. This demo will focus on two general data representations:

导入教程 是从工作簿中提取数据的指导示例。强烈建议先查看教程。

¥The Import Tutorial is a guided example of extracting data from a workbook. It is strongly recommended to review the tutorial first.

测试部署

该浏览器演示在以下环境中进行了测试：

¥This browser demo was tested in the following environments:

浏览器日期
Chromium 1332025-03-30
Safari 18.32025-03-30
Konqueror 222025-04-23

数据表示​

¥Data Representations

许多工作表都包含一个标题行，后跟许多数据行。每行是一个 "observation"，每列是一个 "variable"。

¥Many worksheets include one header row followed by a number of data rows. Each row is an "observation" and each column is a "variable".

"对象数组" 解释使用更惯用的 JavaScript 模式。它适用于较小的数据集。

¥The "Array of Objects" explanations use more idiomatic JavaScript patterns. It is suitable for smaller datasets.

"密集的工作表" 方法性能更高，但代码模式让人想起 C。仅当传统模式速度慢得令人望而却步时，才鼓励使用底层方法。

¥The "Dense Worksheets" approach is more performant, but the code patterns are reminiscent of C. The low-level approach is only encouraged when the traditional patterns are prohibitively slow.

对象数组​

¥Arrays of Objects

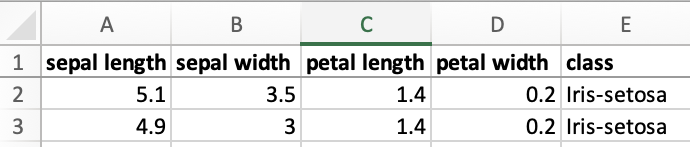
数据集的惯用 JavaScript 表示是一个对象数组。变量名称通常取自第一行。这些名称用作每个观察中的键。

¥The idiomatic JavaScript representation of the dataset is an array of objects. Variable names are typically taken from the first row. Those names are used as keys in each observation.

SpreadsheetJS Data

pres.xlsx data

[
  { Name: "Bill Clinton", Index: 42 },
  { Name: "GeorgeW Bush", Index: 43 },
  { Name: "Barack Obama", Index: 44 },
  { Name: "Donald Trump", Index: 45 },
  { Name: "Joseph Biden", Index: 46 }
]

SheetJS sheet_to_json 方法 [^1] 可以从工作表对象生成对象数组。例如，以下代码片段获取一个测试文件并从第一个工作表创建一个数组数组：

¥The SheetJS sheet_to_json method[^1] can generate arrays of objects from a worksheet object. For example, the following snippet fetches a test file and creates an array of arrays from the first sheet:

const url = "https://xlsx.nodejs.cn/typedarray/iris.xlsx";

/* fetch file and pull file data into an ArrayBuffer */
const file = await (await fetch(url)).arrayBuffer();

/* parse workbook */
const workbook = XLSX.read(file, {dense: true});

/* first worksheet */
const first_sheet = workbook.Sheets[workbook.SheetNames[0]];

/* generate array of arrays */
const aoo = XLSX.utils.sheet_to_json(first_sheet);

密集的工作表​

¥Dense Worksheets

SheetJS "dense" 工作表 [^2] 将单元格存储在数组的数组中。SheetJS read 方法 [^3] 接受特殊的 dense 选项来创建密集工作表。

¥SheetJS "dense" worksheets[^2] store cells in an array of arrays. The SheetJS read method[^3] accepts a special dense option to create dense worksheets.

以下示例获取文件：

¥The following example fetches a file:

/* fetch file and pull file data into an ArrayBuffer */
const url = "https://xlsx.nodejs.cn/typedarray/iris.xlsx";
const file = await (await fetch(url)).arrayBuffer();

/* parse workbook */
const workbook = XLSX.read(file, {dense: true});

/* first worksheet */
const first_dense_sheet = workbook.Sheets[workbook.SheetNames[0]];

密集工作表的 "!data" 属性是单元格对象 [^4] 数组的数组。单元格对象包括数据类型和值等属性。

¥The "!data" property of a dense worksheet is an array of arrays of cell objects[^4]. Cell objects include attributes including data type and value.

分析变量​

¥Analyzing Variables

可以通过循环对象数组并访问特定键来提取各个变量。例如，使用 Iris 数据集：

¥Individual variables can be extracted by looping through the array of objects and accessing specific keys. For example, using the Iris dataset:

Iris dataset

以下代码片段显示了对象数组中的第一个条目：

¥The following snippet shows the first entry in the array of objects:

{
  "sepal length": 5.1,
  "sepal width": 3.5,
  "petal length": 1.4,
  "petal width": 0.2,
  "class ": "Iris-setosa"
}

可以通过对每个对象建立索引来提取 sepal length 变量的值。以下代码片段打印萼片长度：

¥The values for the sepal length variable can be extracted by indexing each object. The following snippet prints the sepal lengths:

for(let i = 0; i < aoo.length; ++i) {
  const row = aoo[i];
  const sepal_length = row["sepal length"];
  console.log(sepal_length);
}
Result
Loading...
Live Editor
function SheetJSAoOExtractColumn() {
  const [col, setCol] = React.useState([]);

  React.useEffect(() => { (async() => {
    const ab = await (await fetch("/typedarray/iris.xlsx")).arrayBuffer();
    const wb = XLSX.read(ab, {dense: true});
    const aoo = XLSX.utils.sheet_to_json(wb.Sheets[wb.SheetNames[0]]);
    /* store first 5 sepal lengths in an array */
    const col = [];
    for(let i = 0; i < aoo.length; ++i) {
      const row = aoo[i];
      const sepal_length = row["sepal length"];
      col.push(sepal_length); if(col.length >= 5) break;
    }
    setCol(col);
  })(); }, []);

  return ( <>
  <b>First 5 Sepal Length Values</b><br/>
  <table><tbody><tr>{col.map(sw => (<td>{sw}</td>))}</tr></tbody></table>
  </>
  );
}

平均值​

¥Average (Mean)

对于给定的数字序列 x1…xcountx_1\mathellipsis x_{count}，平均值 MM 定义为元素之和除以计数：

¥For a given sequence of numbers x1…xcountx_1\mathellipsis x_{count} the mean MM is defined as the sum of the elements divided by the count:

M[x;count]=1count∑i=1countxiM[x;count] = \frac{1}{count}\sum_{i=1}^{count} x_i

用 JavaScript 术语来说，数组的平均值是数组中数字的总和除以数值总数。

¥In JavaScript terms, the mean of an array is the sum of the numbers in the array divided by the total number of numeric values.

非数字元素和数组孔不会影响总和，也不会对计数产生影响。算法应显式跟踪计数，并且不能假设数组 length 属性将是正确的计数。

¥Non-numeric elements and array holes do not affect the sum and do not contribute to the count. Algorithms are expected to explicitly track the count and cannot assume the array length property will be the correct count.

该定义与电子表格 AVERAGE 函数一致。

¥This definition aligns with the spreadsheet AVERAGE function.

AVERAGEA 与 AVERAGE 的不同之处在于对字符串和布尔值的处理：字符串值被视为零，布尔值映射到它们的强制数字等效项（true 是 1，false 是 0）。

¥AVERAGEA differs from AVERAGE in its treatment of string and Boolean values: string values are treated as zeroes and Boolean values map to their coerced numeric equivalent (true is 1 and false is 0).

JavaScript 生态系统

一些 JavaScript 库实现了计算数组均值的函数。

¥Some JavaScript libraries implement functions for computing array means.

库执行
jStat[^8]课本总和（最后除以）
simple-statistics[^9]Neumaier 补偿金额（最后除）
stdlib.js[^10]试验平均值 (mean) / van Reeken (incrmean)

文本薄总和​

¥Textbook Sum

可以通过计算总和并除以计数来计算一系列值的平均值。

¥The mean of a sequence of values can be calculated by computing the sum and dividing by the count.

以下函数接受一个对象数组和一个键。

¥The following function accepts an array of objects and a key.

function aoa_average_of_key(aoo, key) {
  let sum = 0, cnt = 0;
  for(let R = 0; R < aoo.length; ++R) {
    const row = aoo[R];
    if(typeof row == "undefined") continue;

    const field = row[key];
    if(typeof field != "number") continue;

    sum += field; ++cnt;
  }
  return cnt == 0 ? 0 : sum / cnt;
}
Live Demo (click to show)
Result
Loading...
Live Editor
function SheetJSAoOAverageKey() {
  const [avg, setAvg] = React.useState(NaN);

  function aoa_average_of_key(aoo, key) {
    let sum = 0, cnt = 0;
    for(let R = 0; R < aoo.length; ++R) {
      const row = aoo[R];
      if(typeof row == "undefined") continue;

      const field = row[key];
      if(typeof field != "number") continue;

      sum += field; ++cnt;
    }
    return cnt == 0 ? 0 : sum / cnt;
  }

  React.useEffect(() => { (async() => {
    const ab = await (await fetch("/typedarray/iris.xlsx")).arrayBuffer();
    const wb = XLSX.read(ab, {dense: true});
    const aoo = XLSX.utils.sheet_to_json(wb.Sheets[wb.SheetNames[0]]);
    setAvg(aoa_average_of_key(aoo, "sepal length"));
  })(); }, []);

  return ( <b>The average Sepal Length is {avg}</b> );
}

当对许多相似大小的值求和时，教科书方法会遇到数值问题。随着元素数量的增加，总和的绝对值会比各个值的绝对值大几个数量级，并且有效数字会丢失。

¥The textbook method suffers from numerical issues when many values of similar magnitude are summed. As the number of elements grows, the absolute value of the sum grows to orders of magnitude larger than the absolute values of the individual values and significant figures are lost.

van Reeken​

教科书方法中的一些问题可以通过微分技术来解决。可以计算并更新平均值的估计，而不是计算总和。

¥Some of the issues in the textbook approach can be addressed with a differential technique. Instead of computing the whole sum, it is possible to calculate and update an estimate for the mean.

van Reeken 数组均值可以用一行 JavaScript 代码实现：

¥The van Reeken array mean can be implemented in one line of JavaScript code:

for(var n = 1, mean = 0; n <= x.length; ++n) mean += (x[n-1] - mean)/n;
Math details (click to hide)

令 M[x;m]=1m∑i=1mxiM[x;m] = \frac{1}{m}\sum_{i=1}^{m}x_i 为前 mm 个元素的平均值（其中 m>0m > 0）。前 m+1m+1 个元素的平均值遵循一个简单的关系：

¥Let M[x;m]=1m∑i=1mxiM[x;m] = \frac{1}{m}\sum_{i=1}^{m}x_i be the mean of the first mm elements (where m>0m > 0). The mean of the first m+1m+1 elements follows a simple relation:

M[x;m+1]M[x;m+1]

=1m+1∑i=1m+1xi= \frac{1}{m+1}\sum_{i=1}^{m+1} x_i

=1m+1((∑i=1mxi)+xm+1)= \frac{1}{m+1}((\sum_{i=1}^{m} x_i) + x_{m+1})

=1m+1∑i=1mxi+xm+1m+1= \frac{1}{m+1}\sum_{i=1}^{m} x_i + \frac{x_{m+1}}{m+1}

=mm+1(1m∑i=1mxi)+xm+1m+1= \frac{m}{m+1}(\frac{1}{m}\sum_{i=1}^{m} x_i) + \frac{x_{m+1}}{m+1}

=mm+1M[x;m]+xm+1m+1= \frac{m}{m+1}M[x;m] + \frac{x_{m+1}}{m+1}

=(1−1m+1)M[x;m]+xm+1m+1= (1 - \frac{1}{m+1})M[x;m] + \frac{x_{m+1}}{m+1}

=M[x;m]+xm+1m+1−1m+1M[x;m]= M[x;m] + \frac{x_{m+1}}{m+1} - \frac{1}{m+1}M[x;m]

M[x;m+1]M[x;m+1]

=M[x;m]+1m+1(xm+1−M[x;m])= M[x;m] + \frac{1}{m+1}(x_{m+1}-M[x;m])

第一个元素的平均值是 M[x;1]=11∑i=11xi=x1M[x;1] = \frac{1}{1}\sum_{i=1}^{1}x_i = x_1。通过定义 M[x;0]=0M[x;0]=0，递归关系也适用于 m=0m = 0：

¥The mean of the first element is M[x;1]=11∑i=11xi=x1M[x;1] = \frac{1}{1}\sum_{i=1}^{1}x_i = x_1. By defining M[x;0]=0M[x;0]=0, the recurrence relation also holds for m=0m = 0:

x1=0+(x1−0)x_1 = 0 + (x_1 - 0)

=0+11(x1−0)= 0 + \frac{1}{1}(x_1 - 0)

M[x;1]M[x;1]

=M[x;0]+11(x1−M[x;0])= M[x;0] + \frac{1}{1}(x_{1} - M[x;0])

M[x;m+1]M[x;m+1]

=M[x;m]+1m+1(xm+1−M[x;m])= M[x;m] + \frac{1}{m+1}(x_{m+1} - M[x;m])

m=0,M[x;0]=0m = 0, M[x;0] = 0 将作为递归的初始条件。

¥m=0,M[x;0]=0m = 0, M[x;0] = 0 will serve as the initial condition for the recurrence.

JavaScript 从零开始索引：x1x_1 代表 x[0]，通常 xmx_{m} 代表 x[m-1]。

¥JavaScript is zero-indexed: x1x_1 is x[0] and generally xmx_{m} is x[m-1].

调整从零开始的索引后，以下代码计算递归：

¥Adjusting for zero-based indexing, the following code calculates the recurrence:

/* data array */
var x = [ /* ... data ... */ ];

/* initial condition M[x;0] = 0 */
var mean = 0;

/* loop through each value in the array */
for(var m = 0; m < x.length; ++m) {
  /* store the old mean M[x;m] */
  var mean_m  = mean;
  /* get the next data point x_{m+1} */
  var x_m1    = x[m];
  /* calculate the new mean M[x;m+1] */
  var mean_m1 = mean_m + (x_m1 - mean_m) / (m + 1);
  /* update the mean */
  mean = mean_m1;
}

可以通过直接赋值给 mean 来简洁地实现：

¥This can be succinctly implemented by assigning to mean directly:

for(var m = 0, mean = 0; m < x.length; ++m) {
  mean = mean + (x[m] - mean) / (m + 1);
}

可以使用加法赋值运算符 (+=) 进一步简化：

¥This can be condensed further by using the addition assignment (+=) operator:

for(var m = 0, mean = 0; m < x.length; ++m) mean += (x[m] - mean) / (m + 1);

替换 n = m+1 得到最终代码表达式：

¥Replacing n = m+1 yields the final code expression:

for(var n = 1, mean = 0; n <= x.length; ++n) mean += (x[n-1] - mean) / n;

以下函数接受一个对象数组和一个键。

¥The following function accepts an array of objects and a key.

function aoa_mean_of_key(aoo, key) {
  let mean = 0, cnt = 0;
  for(let R = 0; R < aoo.length; ++R) {
    const row = aoo[R];
    if(typeof row == "undefined") continue;

    const field = row[key];
    if(typeof field != "number") continue;

    mean += (field - mean) / ++cnt;
  }
  return cnt == 0 ? 0 : mean;
}
Live Demo (click to show)
Result
Loading...
Live Editor
function SheetJSAoOMeanKey() {
  const [avg, setAvg] = React.useState(NaN);

  function aoa_mean_of_key(aoo, key) {
    let mean = 0, cnt = 0;
    for(let R = 0; R < aoo.length; ++R) {
      const row = aoo[R];
      if(typeof row == "undefined") continue;

      const field = row[key];
      if(typeof field != "number") continue;

      mean += (field - mean) / ++cnt;
    }
    return cnt == 0 ? 0 : mean;
  }

  React.useEffect(() => { (async() => {
    const ab = await (await fetch("/typedarray/iris.xlsx")).arrayBuffer();
    const wb = XLSX.read(ab, {dense: true});
    const aoo = XLSX.utils.sheet_to_json(wb.Sheets[wb.SheetNames[0]]);
    setAvg(aoa_mean_of_key(aoo, "sepal length"));
  })(); }, []);

  return ( <b>The average Sepal Length is {avg}</b> );
}
历史背景

该算法一般归因于 Welford[^11]。然而，原论文并没有提出这种计算均值的算法！

¥This algorithm is generally attributed to Welford[^11]. However, the original paper does not propose this algorithm for calculating the mean!

包括 Neely[^12] 在内的程序员将一种不同的算法归因于 Welford。van Reeken[^13] 报告了本节中介绍的算法的成功。

¥Programmers including Neely[^12] attributed a different algorithm to Welford. van Reeken[^13] reported success with the algorithm presented in this section.

Knuth[^14] 错误地将平均值的实现归因于 Welford。

¥Knuth[^14] erroneously attributed this implementation of the mean to Welford.

"半数值算法"（TAOCP 第 2 卷）中的错误已解决！[^15]

¥The error in "Seminumerical Algorithms" (TAOCP Volume 2) was addressed![^15]

SheetJS 队友已收到 Knuth 奖励支票以表彰其贡献。

¥A SheetJS teammate has received a Knuth Reward Check for the contribution.

[^1]: 见 sheet_to_json 于 "实用工具"

¥See sheet_to_json in "Utilities"

[^2]: 见 "密集模式" 于 "实用工具"

¥See "Dense Mode" in "Utilities"

[^3]: 见 read 于 "读取文件"

¥See read in "Reading Files"

[^4]: 见 "密集模式" 于 "实用工具"

¥See "Dense Mode" in "Utilities"

[^5]: 见 "单元格类型" 于 "单元格对象"

¥See "Cell Types" in "Cell Objects"

[^6]: 见 "基本值" 于 "单元格对象"

¥See "Underlying Values" in "Cell Objects"

[^7]: 见 "单元格类型" 于 "单元格对象"

¥See "Cell Types" in "Cell Objects"

[^8]: 请参阅 jStat 文档中的 mean()。

¥See mean() in the jStat documentation.

[^9]: 请参阅 simple-statistics 文档中的 mean。

¥See mean in the simple-statistics documentation.

[^10]: 请参阅 stdlib.js 文档中的 incrsum。

¥See incrsum in the stdlib.js documentation.

[^11]: 请参阅《Technometrics》第 4 卷第 3 卷（1962 年 8 月）中的 "关于计算校正平方和和乘积的方法的注释"。

¥See "Note on a Method for Calculated Corrected Sums of Squares and Products" in Technometrics Vol 4 No 3 (1962 August).

[^12]: 参见 CACM 第 9 卷第 7 期中的 "几种计算均值、标准差和相关系数的算法比较"（1966 年 7 月）。

¥See "Comparison of Several Algorithms for Computation of Means, Standard Deviations and Correlation Coefficients" in CACM Vol 9 No 7 (1966 July).

[^13]: 参见 CACM 第 11 卷第 3 期（1968 年 3 月）中的 "处理尼利算法"。

¥See "Dealing with Neely's Algorithms" in CACM Vol 11 No 3 (1968 March).

[^14]: 请参阅“计算机编程的艺术：半数值算法”第三版第 232 页。

¥See "The Art of Computer Programming: Seminumerical Algorithms" Third Edition page 232.

[^15]: 查看 TAOCP 站点中的 "第 2 卷勘误表（2021 年之后）"

¥See the "Errata for Volume 2 (after 2021)" in the TAOCP site